Avec ESSEC Knowledge Editor-in-chief
« Big Data », « statistiques de en grande dimension », « analyse prédictive »... si nous avons probablement tous entendu au moins un de ces termes, leur signification est peut-être un peu plus floue difficile à comprendre. Comment sont-ils appliqués ? Comment les progrès de l’analyse des données peuvent-ils avoir un impact sur notre vie quotidienne ? Olga Klopp, professeur à l’ESSEC, et sa collègue Geneviève Robin de l’École des Ponts ParisTech ont développé une nouvelle méthode d’imputation des données pour répondre aux défis de l’analyse des données modernes.
Pour que les données puissent être analysées, elles doivent d’abord être transformées de leur forme brute en un format plus utilisable. Nous faisons cela de multiples façons chaque jour : nous regardons le visage d’une personne et pouvons identifier la combinaison de traits comme ceux de nos collègues ou amis, nous entendons un son et l’identifions comme étant un klaxon ... nous sentons une odeur dans l’air et nous réalisons qu’il y a une boulangerie à proximité. Nous transformons également des données dans le cadre de nos activités professionnelles : un médecin prend une liste de symptômes et la « transforme » en un diagnostic et un pronostic. Pour que ce dernier se produise, nous devons être capables de prédire: en d’autres termes, de prévoir quelque chose que nous n’avons pas observé, sur la base des données que nous avons observées. Pensez, par exemple, à un patient qui a eu un grave accident de voiture. Cette personne risque un choc hémorragique qui mettrait sa vie en danger. La détection précoce du choc hémorragique permet donc de mieux traiter les patients concernés et, dans certains cas, d’éviter leur décès. Les médecins ont identifié un certain nombre de facteurs associés au choc hémorragique : en d’autres termes, ils prédisent un trait non observé (le choc) à partir d’une série de traits observés (par exemple, le niveau d’hémoglobine de la personne). Cependant, la réalité est un peu plus compliquée, car la précision de cette prédiction est liée à trois hypothèses. Les trois hypothèses sont : que l’on dispose d’information a priori sur le phénomène que l’on cherche à décrire, que l’on dispose de données antérieures et que l’on dispose d’un modèle permettant de synthétiser et d’interpréter ces données. Il n’est pas toujours possible de vérifier ces hypothèses. Souvent, nous nous intéressons à un phénomène pour lequel nous ne savons pas encore quels indicateur, trait ou facteur sont liés à celui-ci. Par exemple, dans l’étude génomique du cancer, où l’on cherche à identifier des gènes potentiellement reliés au développement d’un cancer, on dispose en général de mesures faites pour des milliers, voire des millions de gènes, mais on ne sait pas lesquels sont pertinents pour le type de cancer étudié. Cela conduit au problème que l’on appelle en statistique la réduction de la dimensionnalité : à partir d’un grand nombre de variables, peut-on produire un petit nombre d’entre elles qui soient associées au phénomène auquel on s’intéresse ?
Par exemple, disons que nous nous intéressons à trois caractéristiques d’une population : la taille, le poids et un troisième trait qualitatif pour lequel on cherche à distinguer les individus qui le possèdent de ceux qui ne le possèdent pas. Ce trait peut correspondre, par exemple, à la présence d’une maladie ou d’un symptôme particulier. Pour représenter nos données, nous créons un graphique, comme dans la figure 1, où l’axe horizontal représente la taille, l’axe vertical le poids et la couleur du point représente la présence du trait. Nous pouvons voir qu’il existe un lien entre la taille et le poids, les individus les plus grands étant également plus lourds.
La ligne noire représente cette relation linéaire. De plus, le long de cette ligne, on observe que les individus possédant le trait considéré (les points bleus), se trouvent en amont, c’est-à-dire plus proches de l’origine correspondant à un poids et une taille de zéro, que les individus ne possédant pas ce trait (les points rouges). En raison de cette observation, nous n’avons pas besoin de connaître la taille et le poids exact, mais seulement de savoir où ils se situent sur cette ligne, en « résumant » essentiellement les informations fournies par la taille et le poids. Cela est particulièrement utile, car il arrive que nous ne disposions pas de toutes les informations sur un individu, ce qui nous permet de « remplir les blancs », c’est-à-dire d’utiliser l’imputation des données pour compléter les données manquantes. Nous pouvons ensuite créer une troisième variable qui résume ces informations et réaliser le nouveau graphique de la figure 2 : nous avons maintenant une dimension là où nous en avions deux auparavant (taille et poids). En d’autres termes, nous avons réduit la dimensionnalité.
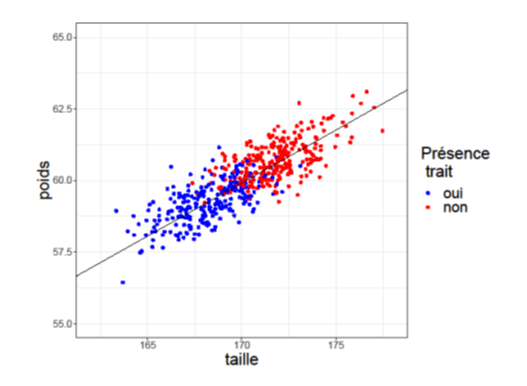
Figure 1. Représentation des individus en fonction de leur poids et leur taille.
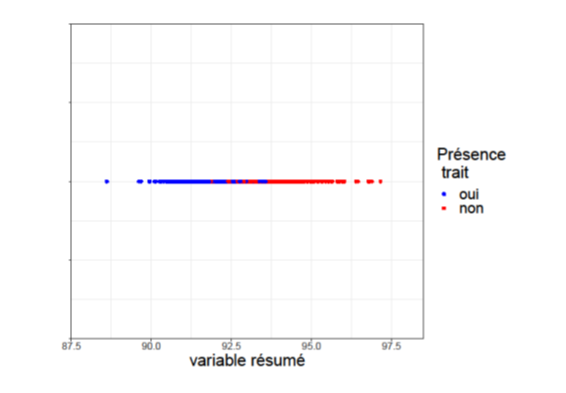
Figure 2. Représentation des individus selon leur positionnement sur la droite noire de la Figure 1.
Et si nous devions prendre en compte plus de deux caractéristiques ? La précision et la valeur prédictive augmentent avec la quantité d’informations incluses : c’est pourquoi les analystes de données cherchent à inclure autant d’informations pertinentes que possible dans leurs modèles. Prenons l’exemple d’un groupe de personnes pour lequel nous disposons de sept variables liées au diabète, que nous voulons utiliser pour prédire si un individu est susceptible de développer le diabète. Comme nous disposons de sept variables, leur représentation graphique est plus complexe et plus difficile à visualiser que dans notre exemple précédent. Cependant, en appliquant les mêmes méthodes de réduction de dimension que ci-dessus, nous pouvons créer, à partir des sept variables quantitatives mesurées, un petit nombre de variables ”résumé”, par exemple deux ou trois, qui peuvent à leur tour être utilisées pour visualiser les données en deux ou trois dimensions.
La réduction des dimensions nous permet de prendre les informations à notre disposition et de les synthétiser dans un format qui peut être interprété plus facilement. Elle facilite l’analyse et l’interprétation en permettant de visualiser les données dans l’espace plutôt que sous la forme d’un tableau. Elle augmente également la précision des méthodes d’imputation des données, ce qui est extrêmement important dans l’analyse des données modernes, car le Big Data est inévitablement “sales” en raison d’informations manquantes ou inexactes. Étant donné la quantité de données à notre disposition, elle a un intérêt computationnel, puisque les variables de synthèse permettent des calculs « plus faciles » (moins intenses et moins longs). Notons que l’analyste a la possibilité de choisir le nombre de dimensions qu’il veut conserver, deux, trois ou plus selon ses besoins, tant que ce nombre ne dépasse pas le nombre de variables initial. Le nombre de dimensions conservées s’appelle le rang. Les méthodes dites de rang faible, c’est-à-dire des méthodes qui permettent de produire un petit nombre de nouvelles variables importantes à partir d’un grand nombre de variables initiales, afin de visualiser et analyser les données plus facilement, jouent un rôle important dans l’analyse des données massives.









